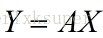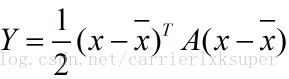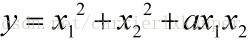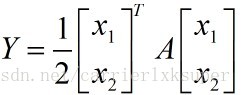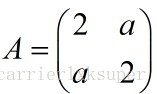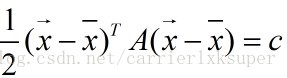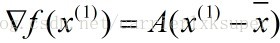On the principle of conjugate gradient method

As a common algorithm in optimization algorithm, conjugate gradient method can be seen in many gradient-optimized machine learning algorithms, such as in sparse coding (sparsenet). This paper mainly refers to the introduction of conjugate gradient in the optimized textbook compiled by Tsinghua University Press, Chen Baolin.

The origin of this article is that I have recently been thinking about a simple function:

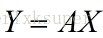
Or a more complex two-time type function: .......... ............... 2, where x is the data center.

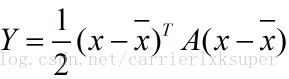
The first question is how to ensure that the output F is always greater than 0, the knowledge of the linear algebra knows that we know the guarantee that the matrix A is positive definite, and if a is semi-positive, then the output is guaranteed to be non-negative. The second problem is the geometric meaning of this two-time function. Let's start with the simplest two-time function, ..... 3

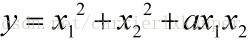
which The Formula 3 is written in the form of Equation 2,

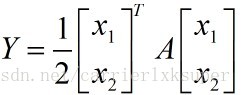
 where. 

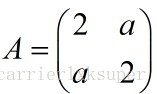
What is the shape of this function? First, in order to guarantee non-negative, we will take a value of -1,0,1 three values respectively. Then, we draw the function shape like →:

In the figure, since A is a 2 * 2 square matrix, we get three three-dimensional surfaces. Surface images are located above the x-y plane, illustrating non-negativity. For each layer, it represents the surface under a different value (a total of 3 layers). And on a certain layer, each contour line (ie contour line) represents a different output value, we have marked it in the figure, we found that the projection of the surface onto the xy plane is an ellipse after rotation ( as follows).

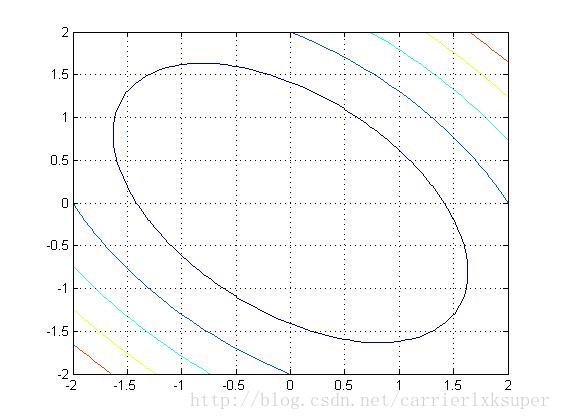
To promote a more general form, when the dimension of A is greater than 2, the super-surface will be obtained, at this time the contour line (accurate is the equivalent surface) in the form of: 

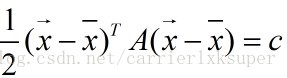
This is the X-drawn as the center of the ellipsoidal surface. Because the gradient at the X-Draw is.

 A positive definite, so X-Pull is the minimum point of the function (remember this is what we want).

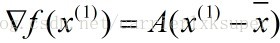
 Suppose there is a point on this ellipsoid (that is, the equivalent plane)

, then at this point, the normal vector of the equivalent plane is, or a two-dimensional example

We assume that D (1) is a tangent vector at the point, and D (2) is a vector of the direction of the line along that point and the center point, i.e.

。 Normal vectors are perpendicular to the plane of any vector, and naturally perpendicular to the tangent vector, we have:

For last equation we say that D (1) and D (2) are conjugated to a.

This is where the gradients and conjugation are finally spoken. For this last equation, we think that the tangent vector at any point on the two-dimensional contour is the vector with this point to the minimum point about a conjugate, which means that the minimum point can be found after two iterations of the two function. For multi-dimensional situations, it is also possible to converge to a minimum point within a finite number of steps. The concrete proof can refer to the textbook.

So when we are looking for the minimum in the optimization, we always look for the minimum point, and we can find the direction to it, find the direction and the direction of the conjugate, and the direction of the conjugate can also be obtained by the direction of the conjugate direction, so push forward in turn, Finally, before starting the conjugate gradient, we first calculate the steepest descent direction of the initial point.

The FR conjugate Gradient method is introduced based on the above ideas. Given an initial point x (1) calculates its gradient d (1), then this d (1) as the tangent vector direction, searches in its direction to get X (2), calculates the gradient G (2) at x (2), uses G (2) and D (1) to construct a new search direction D (2), one time down. This process needs to calculate two quantities, one is the search step for each step, and the other is the direction of the next search. The search step uses a more general formula, and the conjugate is shown when the next search direction is calculated.

Specific algorithm implementation steps and implementation reference: Http://blog.sciencenet.cn/blog-54276-569356.html.